Industry news

保姆级笔记-详细剖析SMO算法中的知识点

序列最小优化算法（Sequential minimal optimization）-SMO算法

SVM算法中原问题的对偶问题是一个凸二次规划问题，同时解这个凸二次规划问题的计算复杂度跟样本的数量有关。当样本数量很大的时候，很多解法就会变的非常低效，以至于无法使用。如何高效的解决这个问题，就是我们要研究的问题。而SMO算法刚好是解决这个问题的好办法。

在开始讲SMO算法之前，我们先介绍一下坐标下降法。大家以前在学梯度下降法的时候，我们总是朝着梯度最大的方向去搜索最优解。而梯度最大的方向，是各个坐标轴方向梯度的向量相加后的那个方向。

而在坐标下降法中，我们把其他几个方向固定，只沿着某一个坐标轴的梯度方向去搜索。因为在一次坐标下降中，我们只有一个变量，所以计算的复杂度大大降低。这样一个复杂的问题，就被分成好多的小问题来解决。

在下图的例子中，我们可以看到，先沿着y轴的方向前进，再固定y沿着x轴的方向前进，最后也能达到最优解的位置。【下面这幅等值线图，我相信大家应该都能看懂，不懂可以留言。】

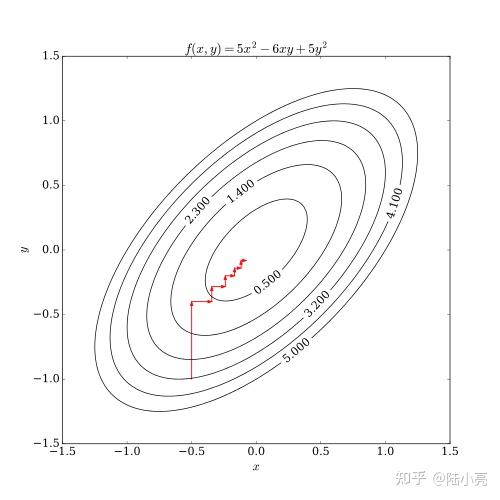
SMO算法跟坐标下降法类似，选择两个变量，固定其他的变量，针对这两个变量构建一个二次规划问题。这个子二次规划问题的解，会更接近原始二次规划问题的解。原因很简单，通过这次子二次规划的求解，会使得原始二次规划问题的目标函数值变的更小。等下给大家展示原始问题的公式，会发现是一个求最小值的问题。如果一组解能够使得问题的值变得更小，那么这组解是不是更接近我们的答案呢？

$min_{\\alpha}\\ \\frac{1}{2}\\sum_{i=1}^{N}{}\\sum_{j=1}^{N}{\\alpha_{i}\\alpha_{j}y_{i}y_{j}(x_{i}\\cdot x_{j})}-\\sum_{i=1}^{N}{\\alpha_{i}}\\\\ s.t.\\ \\sum_{i=1}^{N}{\\alpha_{i}y_{i}}=0\\\\ 0\\leq\\alpha_{i}\\leq C, i=1,2,...,N$

在李航老师的书中p143页， $x_{i}\\cdot x_{j}$ 是用 $K(x_{i}\\cdot x_{j})$ 来表示的，我们后面也会用K来表示，但为了推导更为清楚，我们先这么表示。上述问题已经是软间隔最大化推导过来的，具有一般性。

整个推导过程是记录了大海老师的课程笔记+我自己的理解，大家也可以通过下面的链接直接去看视频，但要完整的看下来，需要耐心。

机器学习 svm_smo算法_哔哩哔哩_bilibili

为了不失一般性，我们选择 $\\alpha_{1}$ 和 $\\alpha_{2}$ 作为我们的变量，其他变量都固定。

这里看着我们是有两个变量 $\\alpha_{1}$ 和 $\\alpha_{2}$ ，但其实他们之间是有约束的，约束是 $\\sum_{i=1}^{N}{\\alpha_{i}y_{i}}=0$ 。所以其实只有一个变量。所以我们这个子问题就是一个一元二次方程的问题，我们可以通过带入消元，把 $\\alpha_{2}$ 消掉来求解函数的最小值。

$令L(\\alpha_{1},\\alpha_{2})=\\frac{1}{2}[\\alpha_{1}y_{1}\\alpha_{1}y_{1}x_{1}^{T}\\cdot x_{1}+2\\alpha_{1}y_{1}\\alpha_{2}y_{2}x_{1}^{T}\\cdot x_{2}+2\\sum_{j=3}^{N}{\\alpha_{1}y_{1}\\alpha_{j}y_{j}x_{1}^{T}\\cdot x_{j}}+\\alpha_{2}y_{2}\\alpha_{2}y_{2}x_{2}^{T}\\cdot x_{2}$

$+2\\sum_{j=3}^{N}{\\alpha_{2}y_{2}\\alpha_{j}y_{j}x_{2}^{T}\\cdot x_{j}}+\\sum_{i=3}^{N}{\\sum_{j=3}^{N}{\\alpha_{i}y_{i}\\alpha_{j}y_{j}x_{i}^{T}\\cdot x_{j}}}]$

$-[\\alpha_{1}+\\alpha_{2}+\\sum_{j=3}^{N}{\\alpha_{j}}]$

我们令 $x_{i}^{T}\\cdot x_{j}=K_{ij}$

$则L(\\alpha_{1},\\alpha_{2})=\\frac{1}{2}[\\alpha_{1}y_{1}\\alpha_{1}y_{1}K_{11}+2\\alpha_{1}y_{1}\\alpha_{2}y_{2}K_{12}+2\\sum_{j=3}^{N}{\\alpha_{1}y_{1}\\alpha_{j}y_{j}K_{1j}}+\\alpha_{2}y_{2}\\alpha_{2}y_{2}K_{22}$

$+2\\sum_{j=3}^{N}{\\alpha_{2}y_{2}\\alpha_{j}y_{j}K_{2j}}+\\sum_{i=3}^{N}{\\sum_{j=3}^{N}{\\alpha_{i}y_{i}\\alpha_{j}y_{j}K_{ij}}}]$

$-[\\alpha_{1}+\\alpha_{2}+\\sum_{j=3}^{N}{\\alpha_{j}}]$

进一步化简，其中 $\\sum_{i=3}^{N}{\\sum_{j=3}^{N}{\\alpha_{i}y_{i}\\alpha_{j}y_{j}K_{ij}}}$ 和 $\\sum_{j=3}^{N}{\\alpha_{j}}$ 是常数，我们在后面的式子中把他们省略，因为他们不影响我们求导。

$L(\\alpha_{1},\\alpha_{2})=\\frac{1}{2}[\\alpha_{1}^{2}K_{11}+2\\alpha_{1}y_{1}\\alpha_{2}y_{2}K_{12}+2\\sum_{j=3}^{N}{\\alpha_{1}y_{1}\\alpha_{j}y_{j}K_{1j}}+\\alpha_{2}^{2}K_{22}+2\\sum_{j=3}^{N}{\\alpha_{2}y_{2}\\alpha_{j}y_{j}K_{2j}}]$

$-[\\alpha_{1}+\\alpha_{2}]$

$∵\\sum_{i=1}^{N}{\\alpha_{i}y_{i}}=0 \\Rightarrow \\alpha_{1}y_{1}+\\alpha_{2}y_{2}+\\sum_{i=3}^{N}{\\alpha_{i}y_{i}}=0$

$∵ \\alpha_{i}(i>=3)$ 是固定的，所以 $\\alpha_{1}y_{1}+\\alpha_{2}y_{2}-\\varsigma=0 \\Rightarrow \\ \\alpha_{1}y_{1}+\\alpha_{2}y_{2}=\\varsigma$

$∴ \\alpha_{1}=y_{1}(\\varsigma-\\alpha_{2}y_{2}), 其中y_{1}y_{1}=1$

我们把 $\\alpha_{1}=y_{1}(\\varsigma-\\alpha_{2}y_{2})$ 带入 $L^{'}(\\alpha_{1},\\alpha_{2})$ , 得：

$L(\\alpha_{2})=\\frac{1}{2}[(\\varsigma-\\alpha_{2}y_{2})^{2}K_{11}+2(\\varsigma-\\alpha_{2}y_{2})\\alpha_{2}y_{2}K_{12}+2\\sum_{j=3}^{N}{(\\varsigma-\\alpha_{2}y_{2})\\alpha_{j}y_{j}K_{1j}}+\\alpha_{2}^{2}K_{22}+2\\sum_{j=3}^{N}{\\alpha_{2}y_{2}\\alpha_{j}y_{j}K_{2j}}]$

$-[y_{1}(\\varsigma-\\alpha_{2}y_{2})+\\alpha_{2}]$

我们要求最小值，对于一元二次方程，我们就是求导。

$\\frac{\\sigma L}{\\sigma \\alpha_{2}}=$ $\\frac{1}{2}[-2y_{2}(\\varsigma-\\alpha_{2}y_{2})K_{11}+(2\\varsigma y_{2}K_{12}-4\\alpha_{2}K_{12})-2\\sum_{I=3}^{n}{y_{2}\\alpha_{i}y_{i}K_{1i}}$

$+2\\alpha_{2}K_{22}+2\\sum_{i=3}^{N}{y_{2}\\alpha_{j}y_{j}K_{2j}}]-[-y_{1}y_{2}+1]$

再化简

$\\frac{\\sigma L}{\\sigma \\alpha_{2}}=$ $y_{1}y_{2}-1$ $-\\varsigma y_{2}K_{11}+\\alpha_{2}K_{11}$ $+\\varsigma y_{2}K_{12}-2\\alpha_{2}K_{12}$ $+\\alpha_{2}K_{22}$ $-\\sum_{i=3}^{n}{y_{2}\\alpha_{i}y_{i}K_{1i}}$ $+\\sum_{i=3}^{N}{y_{2}\\alpha_{j}y_{j}K_{2j}}=0$

$\\alpha_{2}(K_{11}+K_{22}-2K_{12})=$ $1-y_{1}y_{2}$ $+\\varsigma y_{2}K_{11}$ $-\\varsigma y_{2}K_{12}$ $+\\sum_{i=3}^{N}{y_{2}\\alpha_{i}y_{i}K_{1i}}$ $-\\sum_{i=3}^{N}{y_{2}\\alpha_{j}y_{j}K_{2j}}$

$=y_{2}[$ $y_{2}$ $-y_{1}$ $+\\varsigma K_{11}$ $-\\varsigma K_{12}$ $+\\sum_{i=3}^{N}{\\alpha_{i}y_{i}K_{1i}}$ $-\\sum_{i=3}^{N}{\\alpha_{i}y_{i}K_{2i}}]\\ (公式1)$

在SVM对偶算法中（李航老师的书p120页），我们有一个结论， $w=\\sum_{i=1}^{N}{\\alpha_{i}y_{i}x_{i}}$

又因为 $f(x)=w^{T}*x+b$ ,所以 $f(x)=\\sum_{i=1}^{N}{\\alpha_{i}y_{i}x_{i}^{T}}*x+b$

所以 $f(x_{1})=\\sum_{i=1}^{N}{\\alpha_{i}y_{i}x_{i}}*x_{1}+b=\\alpha_{1}y_{1}x_{1}^{T}*x_{1}+\\alpha_{2}y_{2}x_{2}^{T}*x_{1}+\\sum_{i=3}^{N}{\\alpha_{i}y_{i}x_{i}}*x_{1}+b$

所以 $f(x_{1})-$ $\\alpha_{1}y_{1}x_{1}^{T}*x_{1}-\\alpha_{2}y_{2}x_{2}^{T}*x_{1}-b=$ $\\sum_{i=3}^{N}{\\alpha_{i}y_{i}x_{i}}*x_{1}$ ，又因为有 $x_{i}^{T}\\cdot x_{j}=K_{ij}$ ，

所以 $f(x_{1})-\\alpha_{1}y_{1}K_{11}-\\alpha_{2}y_{2}K_{12}-b=\\sum_{i=3}^{N}{\\alpha_{i}y_{i}K_{1i}}\\ (公式2)$

同理 $f(x_{2})-\\alpha_{1}y_{1}K_{12}-\\alpha_{2}y_{2}K_{22}-b=\\sum_{i=3}^{N}{\\alpha_{i}y_{i}K_{2i}}\\ (公式3)$

我们把公式1和公式2，带入到公式1中，得

$\\alpha_{2}(K_{11}+K_{22}-2K_{12})=y_{2}[y_{2}-y_{1}+\\varsigma K_{11}-\\varsigma K_{12}+f(x_{1})-\\alpha_{1}y_{1}K_{11}-\\alpha_{2}y_{2}K_{12}-b$

$-f(x_{2})+\\alpha_{1}y_{1}K_{12}+\\alpha_{2}y_{2}K_{22}+b]\\ 公式(4)$

那这里有个常量 $\\varsigma$ ， $\\varsigma$ 等于多少呢？我们说SMO算法其实是个迭代的算法，我们会给 $\\alpha_{1}和\\alpha_{2}$ 附上初始值为 $\\alpha_{1}^{old}和\\alpha_{2}^{old}$ ，从前面的推导可知 $\\alpha_{1}y_{1}+\\alpha_{2}y_{2}=\\varsigma$

所以 $\\alpha_{1}^{old}y_{1}+\\alpha_{2}^{old}y_{2}=\\varsigma$ ,带入公式4, 得

$\\alpha_{2}(K_{11}+K_{22}-2K_{12})=y_{2}[y_{2}-y_{1}+\\alpha_{1}^{old}y_{1}K_{11}-\\alpha_{2}^{old}y_{2}K_{11}-\\alpha_{1}^{old}y_{1}K_{12}-\\alpha_{2}^{old}y_{2}K_{12}$ $+f(x_{1})-\\alpha_{1}^{old}y_{1}K_{11}-\\alpha_{2}^{old}y_{2}K_{12}-b$ $-f(x_{2})+\\alpha_{1}^{old}y_{1}K_{12}+\\alpha_{2}^{old}y_{2}K_{22}+b]\\ 公式(5)$

$=$ $y_{2}[y_{2}-y_{1}$ $+\\alpha_{2}^{old}y_{2}K_{11}$ $+f(x_{1})$ $-2\\alpha_{2}^{old}y_{2}K_{12}$ $-f(x_{2})$ $+\\alpha_{2}^{old}y_{2}K_{22}]$ 公式（6）

如下图做合并同类项, 得公式6

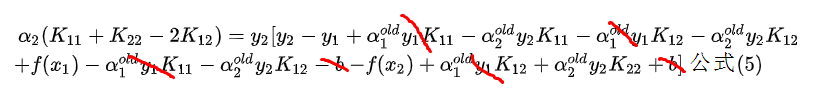
经过整理，公式6为：

$\\alpha_{2}^{new,unc}(K_{11}+K_{22}-2K_{12})=$ $y_{2}[(f(x_{1})-y_{1})-(f(x_{2})-y_{2})+$ $+\\alpha_{2}^{old}y_{2}(K_{11}+K_{22}-2K_{12})]$

$令E_{1}=f(x_{1})-y_{1},\\ E_{2}=f(x_{2})-y_{2}, \\eta=K_{11}+K_{22}-2K_{12}$

$所以\\alpha_{2}^{new,unc}=\\alpha_{2}^{old}+\\frac{y_{2}(E_{1}-E_{2})}{\\eta}$

在上述推导中求得的 $\\alpha_{2}^{new}$ 是未经过剪辑的，我们记作 $\\alpha_{2}^{new,unc}$ 。剪辑过的记作 $\\alpha_{2}^{new}$

什么叫做未剪辑呢？很多同学看书的时候是有疑惑的，下面我们来解释一下。

首先 $\\alpha_{2}^{new,unc}$ 是我们通过求导数为0，而得到的极值点。

通过条件 $\\alpha_{1}y_{1}+\\alpha_{2}y_{2}=\\varsigma$ ，我们可知 $\\alpha_{2}$ 的取值是有约束的，换句话说 $\\alpha_{2}$ 的取值是有范围的。 $\\alpha_{2}^{new,unc}$ 的取值能落在 $\\alpha_{2}$ 的取值范围内吗？

我们假设L是 $\\alpha_{2}$ 取值的下界，H是 $\\alpha_{2}$ 取值的上界，即 $L\\leq\\ \\alpha^{new}\\leq H$

举例：

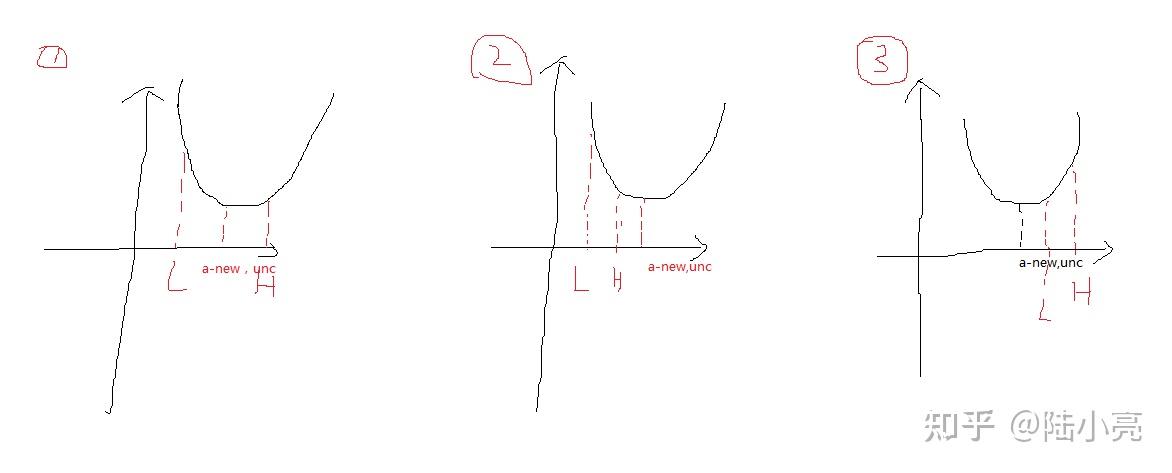
从上图中我们可以看出，当函数取最小值的点是最优解：

第一种情况： $\\alpha_{2}^{new}=\\alpha_{2}^{new,unc}$ ,当 $L\\leq \\alpha_{2}^{new,unc}\\leq H$

第二种情况： $\\alpha_{2}^{new}=H$ ，当 $\\alpha_{2}^{new,unc}> H$

第三种情况： $\\alpha_{2}^{new}=L$ , 当 $\\alpha_{2}^{new,unc}<L$

我们分两种情况进行讨论:

前提： $\\alpha_{1}y_{1}+\\alpha_{2}y_{2}=\\varsigma$

情况1： $y_{1}\ e y_{2}\\Rightarrow\\ y_{1}和y_{2}是异号\\Rightarrow \\alpha_{1}-\\alpha_{2}=k$ (根据y1和y2取值的不同，k可能等于 $\\varsigma$ 或者 $-\\varsigma$ )

因为 $\\alpha_{1}\\subseteq[0,C]$ , $\\alpha_{2}=\\alpha_{1}-k$

所以 $\\alpha_{2}\\subseteq[-k,C-k]=[\\alpha_{2}-\\alpha_{1},C+\\alpha_{2}-\\alpha_{1}]$

又因为 $\\alpha_{2}\\subseteq[0,C]$

所以要取交集，则 $L=max(0,\\alpha_{2}^{old}-\\alpha_{1}^{old})$ , $H=min(C,C+\\alpha_{2}^{old}-\\alpha_{1}^{old})$

情况2： $y_{1}=y_{2}\\Rightarrow \\alpha_{1}+\\alpha_{2}=k$

因为 $\\alpha_{1}\\subseteq[0,C]$ , $\\alpha_{2}=k-\\alpha_{1}，-\\alpha_{1}\\subseteq[-C,0]$

所以 $\\alpha_{2}\\subseteq[k-C,k]=[\\alpha_{1}^{old}+\\alpha_{2}^{old}-C,\\alpha_{1}^{old}+\\alpha_{2}^{old}]$

又因为 $\\alpha_{2}\\subseteq[0,C]$

所以要取交集，则 $L=max(0,\\alpha_{1}^{old}+\\alpha_{2}^{old}-C)$ , $H=min(C,\\alpha_{1}^{old}+\\alpha_{2}^{old})$

SMO方法中的核心就是选取两个 $\\alpha$ ，但我们有N个 $\\alpha$ ，如何从中选取两个呢？

核心思想就是至少选择一个变量是违反KKT条件的。那怎么样算违反了KKT条件呢？反过来理解，就是怎么样算满足KKT条件呢？

软间隔最大化的原问题:

$min_{w,b,\\varepsilon}\\ \\frac{1}{2}\\left| w \\right|^2+C\\sum_{i=1}^{N}{\\varepsilon_{i}}$ , $\\varepsilon_{i}$ 为松弛变量，C为惩罚函数

$s.t.\\ y_{i}(\\omega\\cdot x_{i}+b)\\geq 1-\\varepsilon_{i},i=1,2,...,N$

$\\varepsilon_{i}\\geq0,i=1,2,...,N$

我们改写成最优化问题的标准形式：

$min_{w,b,\\varepsilon}\\ \\frac{1}{2}\\left| w \\right|^2+C\\sum_{i=1}^{N}{\\varepsilon_{i}}$ , $\\varepsilon_{i}$ 为松弛变量，C为惩罚函数

$s.t.\\ 1-\\varepsilon_{i}-y_{i}(\\omega\\cdot x_{i}+b)\\leq0,i=1,2,...,N$

$-\\varepsilon_{i}\\leq0,i=1,2,...,N$

原始最优化问题的拉格朗日函数是：

$L(w,b,\\varepsilon,\\alpha,\\mu)=\\frac{1}{2}\\left| \\left| x \\right| \\right|^2+C\\sum_{i=1}^{N}{\\varepsilon_{i}}+\\sum_{i=1}^{N}{\\alpha_{i}(1-\\varepsilon_{i}-y_{i}(\\omega\\cdot x_{i}+b))}+\\sum_{i=1}^{N}{-\\mu_{i}\\varepsilon_{i}}$

根据KKT条件可得：

$\\frac{L^{'}}{w^{'}}=w-\\sum_{i=1}^{N}{\\alpha_{i}y_{i}x_{i}}=0$ （1）

$\\frac{L^{'}}{b^{'}}=-\\sum_{i=1}^{N}{\\alpha_{i}y_{i}}=0$ （2）

$\\frac{L^{'}}{\\varepsilon^{'}}=C-\\alpha_{i}-\\mu_{i}=0\\Rightarrow\\ 0\\leq\\alpha_{i}\\leq C$ （3）

$1-\\varepsilon_{i}-y_{i}(\\omega\\cdot x_{i}+b)\\leq0$ （4）

$\\alpha_{i}\\geq0,\\mu_{i}\\geq0$ （5）

$\\alpha_{i}(1-\\varepsilon_{i}-y_{i}(\\omega\\cdot x_{i}+b))=0$ （6）

$\\mu_{i}\\varepsilon_{i}=0$ （7）

根据 $\\alpha_{i}$ 的取值，分情况讨论：

首先我们令 $g(x_{i})=w*x_{i}+b$

当 $\\alpha_{i}=0$ ,根据条件（4），则 $y_{i}(\\omega\\cdot x_{i}+b)\\geq1-\\varepsilon_{i}$ ,有 $y_{i}(\\omega\\cdot x_{i}+b)\\geq1(恒成立)$ $\\Rightarrow y_{i}g(x_{i})\\geq1$

当 $0<\\alpha_{i}<C$ ,根据条件（3）可知 $\\mu_{i}\ e0$ ,再根据条件（7）可知 $\\varepsilon_{i}=0$ ,再根据条件（6）可得 $1-y_{i}(\\omega\\cdot x_{i}+b)=0\\Rightarrow y_{i}g(x_{i})=1$

当 $\\alpha_{i}=C$ ,根据条件（3）得 $\\mu_{i}=0$ ,再根据条件（7）可知 $\\varepsilon_{i}>=0$ ,再根据条件（6）可得 $1-\\varepsilon_{i}=y_{i}(\\omega\\cdot x_{i}+b)$ ，所以 $y_{i}(\\omega\\cdot x_{i}+b)\\leq1\\Rightarrow y_{i}g(x_{i})\\leq1$

所以满足KKT条件，就可以用下列式子进行判断（简化以后的式子方便编程啊）：

$当\\alpha_{i}=0,y_{i}g(x_{i})\\geq1$

$当0<\\alpha_{i}<C,y_{i}g(x_{i})=1$

$当\\alpha_{i}=C,y_{i}g(x_{i})\\leq1$

SMO称选择第一个变量的过程为外层循环。外层循环在训练样本中选取违反KKT条件最严重的样本点，并将其对应的变量作为第一个变量。

首先遍历 $0<\\alpha_{i}<C$ 的样本点，即在间隔边界上的支持向量点，检验他们是否满足KKT条件。如果都满足，则遍历整个训练集，检验它们是否满足KKT条件。

SMO将第二个变量的选择过程成为内循环。假设外层循环已经找到了第一个变量 $\\alpha_{1}$ ,现在要在内层循环中找第二个变量 $\\alpha_{2}$ 。而第二个变量选择的标准就是希望 $\\alpha_{2}$ 能有足够大的变化。而我们根据前面的推导可得：

$\\alpha_{2}^{new,unc}=\\alpha_{2}^{old}+\\frac{y_{2}(E_{1}-E_{2})}{\\eta}$

所以 $\\alpha_{2}$ 依赖于 $E_{1}-E_{2}$ 。

那我们选择一种最简单的方法，我们找到一个 $\\alpha_{2}$ ,使得 $\\left| E_{1}-E_{2}\\right|$ 最大。

如果遇到特殊的情况，内层循环通过上述方法选择的 $\\alpha_{2}$ 不能使目标函数有足够的下降，那就采用启发式规则继续选择 $\\alpha_{2}$ 。首先遍历在间隔边界上的支持向量点，依次作为 $\\alpha_{2}$ 试用，直到目标函数有足够的下降。若这样还找不到，那就遍历整个训练集。若仍然还是找不到，则放弃第一个 $\\alpha_{1}$ ，重新找一个新的 $\\alpha_{1}$ 。

完成两个变量的优化后，都需要重新计算b

当 $0<\\alpha_{1}^{new}<C$ ,可知 $y_{i}g(x_{i})=1$ ，得 $\\sum_{i=1}^{N}{\\alpha_{i}y_{i}K_{i1}}+b=y_{1}$ ,

于是 $b_{1}^{new}=y_{1}-\\sum_{i=3}^{N}{\\alpha_{i}y_{i}K_{i1}}-\\alpha_{1}^{new}y_{1}K_{11}-\\alpha_{2}^{new}y_{2}K_{21}$ （1）

根据E1的定义 $E_{1}=g(x_{1})-y_{1}=\\sum_{i=3}^{N}{\\alpha_{i}y_{i}K_{1i}}+\\alpha_{1}^{old}y_{1}K_{11}+\\alpha_{2}^{old}y_{2}K_{21}+b^{old}-y_{1}$ （2）

所以 $y_{1}-\\sum_{i=3}^{N}{\\alpha_{i}y_{i}K_{1i}}=-E_{1}+\\alpha_{1}^{old}y_{1}K_{11}+\\alpha_{2}^{old}y_{2}K_{21}+b^{old}$ （3），带入（1）中

得 $b_{1}^{new}=-E_{1}-y_{1}K_{11}(\\alpha_{1}^{new}-\\alpha_{1}^{old})-y_{2}K_{21}(\\alpha_{2}^{new}-\\alpha_{2}^{old})+b^{old}$

同理，如果 $0<\\alpha_{2}<C$ ,则

$b_{2}^{new}=-E_{2}-y_{1}K_{12}(\\alpha_{1}^{new}-\\alpha_{1}^{old})-y_{2}K_{22}(\\alpha_{2}^{new}-\\alpha_{2}^{old})+b^{old}$

如果 $\\alpha_{1}^{new}和\\alpha_{2}^{new}都满足0<\\alpha_{i}^{new}<C$ ,则 $b_{1}^{new}=b_{2}^{new}$

如果 $\\alpha_{1}^{new}和\\alpha_{2}^{new}是0或者C，则选择他们的中点为b^{new}$

还要更新 $E_{i}$ , $E_{i}^{new}=\\sum_{S}^{}{y_{j}\\alpha_{j}K(x_{i},x_{j})}+b^{new}-y_{i}$ ,其中S为所有支持向量点 $x_{j}$ 的集合。

优化算法——坐标下降法(Coordinate Descent) - 知乎

ARGO创新实验室：优化算法——坐标下降法(Coordinate Descent)

快速理解SMO算法_哔哩哔哩_bilibili

机器学习 svm_smo算法_哔哩哔哩_bilibili

SMO算法的推导与python实现 - 知乎

葛溪驿：SMO算法的推导与python实现

PREVIOUS：抖音直播基地申请条件有哪些？ NEXT：电竞圈恶霸,铁血、未来、古典,小钰,余霜,rita,全本TXT下载,小说txt下载

耀世新闻

Contact Us

Contact: 耀世-耀世平台-耀世全球商务站

Phone: 13800000000

Tel: 400-123-4567

E-mail: admin@youweb.com

Add: Here is your company address

Industry news

保姆级笔记-详细剖析SMO算法中的知识点

Related News

Categories

耀世新闻

Contact Us